Schița subiectului

  • General

    Restrânge toate secțiunile Extinde toate secțiunile

  • MathType pentru Moodle

    MathType, un editor online pentru scriere de formule matematice și chimice, este integrat în platforma Moodle printr-un plugin care extinde bara de instrumente a editorului de text.

    Creați conținut cu formule pentru STEM folosind MathType integrat în Moodle.

  • WirisQuizzes

    WirisQuizzes vine ca un plugin pentru Moodle, ceea ce face ca instalarea sa să fie foarte ușor de efectuat.

    Înlăturați limitările tipice pe care le au chestionarele standard și furnizați adevărate evaluări STEM folosind parametri aleatori, grafice și multe altele.

    WirisQuizzes for Moodle va fi partenerul dvs. perfect pentru a îmbunătăți procesul de învățare al studenților cu feedback în timp real.

     

    • Pentru Profesori

      Descoperiți cum WirisQuizzes extinde posibilitățile de evaluare în domeniul Matematică și STEM în platforma dvs. Moodle.

    • Îmbunătățirea calității temelor STEM

      Eficientizați evaluarea cunoștințele conceptuale ale studenților cu ajutorul capacității instrumentului WIRIS de a compune și evalua întrebări deschise la care studenții răspund.

    • Treceți dincolo de întrebările cu alegeri multiple

      Creați teste cu parametri aleatori și dinamici făcând mai dinamică evaluarea STEM în mediul online.

    • Instrument grafic

      Utilizați instrumentul grafic pentru a testa înțelegerea studenților asupra reprezentărilor funcțiilor sau a teoremelor din geometrie.

    • Atenuează trișarea

      Atenuați modalitățile de trișare cu WirisQuizzes! Utilizarea variabilelor aleatorii vă asigură că fiecare student va primi un test diferit.

    • Economisiți timp

      Economisiți timp cu examenele notate cu tehnologia WirisQuizzes auto-grade. Oferă-ți capacitatea de a petrece mai mult timp predând!

    • Pentru Studenți

      WirisQuizzes se este focusat pe progresului studenților și se asigură că toate conceptele predate sunt pe deplin asimilate și înțeles.

    • Prezentare generală

      Asigurați înțelegerea de către elevi a conceptelor cheie oferindu-le abilitatea de a-și explica raționamentul și de a primi feedback pas cu pas și adaptat la răspunsurile lor.

    • Repetați exercițiile în orice moment

      Cursanții pot folosi abilitatea de a randomiza valorile pentru a repeta același exercițiu, ajutându-i să-și consolideze învățarea.

    • Scris de mână recunoscut

      Răspundeți din mers cu funcția noastră de recunoaștere a scrierii de mână, permițând studenților să răspundă la întrebările STEM de pe tabletele sau dispozitivele lor mobile.

    • Carnet pentru notițe

      Folosiți noul nostru „Scratch-Pad”, permițând elevilor să-și explice raționamentul.

    • Răspundeți cu răspunsuri grafice

      Nu numai că elevii pot răspunde cu limbaj matematic, dar pot răspunde și cu elemente grafice și pot desena funcții.

    • WirisQuizzes este pentru toți

      Îndeplinim cerințele de accesibilitate VPAT pentru a nu lăsa pe nimeni în urmă.
      Un șablon de accesibilitate a produsului voluntar (VPAT ™) este un document care explică modul în care produsele din tehnologia informației și comunicațiilor (TIC), cum ar fi software-ul, hardware-ul, conținutul electronic și documentația de asistență, îndeplinesc (conform) standardelor 508 revizuite pentru accesibilitatea IT.

  • MathType pentru Moodle

    Formule matematice scrise de mână în Moodle cu MathType. Popularul editor de ecuații pentru Microsoft Word și Power Point este acum perfect integrat în Moodle.

    MathType pentru Moodle oferă o experiență de utilizare ușoară, care vă va spori productivitatea. Includeți ecuații și formule matematice în sarcini, întrebări sau comunicări între utilizatori.

    Utilizați bara noastră de instrumente, tastatura sau profitați de dispozitivele cu ecran tactil cu recunoașterea scrierii de mână.

  • Demonstrație

    Fie triunghiul ABC. Notând:

    • O - centrul cercului circumscris triunghiului
    • I - centrul cercului înscris în triunghi
    • R - raza cercului circumscris
    • r - raza cercului înscris
    • d - distanța dinte O și I

    Atunci e valabilă următoarea egalitate:

    d squared equals R open parentheses R minus 2 r close parentheses

    De aici, rezultă și inegalitatea lui Euler:

    R greater or equal than 2 r

  • Funcţia de gradul II

    Definiție.

    Funcția ƒ space colon space R space rightwards arrow space R comma space ƒ open parentheses x close parentheses space equals space a x squared plus b x space plus space c comma space space a comma space b comma space c space element of space R comma space a not equal to 0 se numește funcția de gradul II.

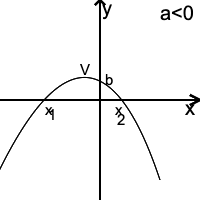
    Reprezentarea geometrică a graficului funcției de gradul II este o parabolă.

          

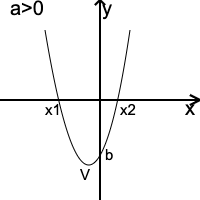
    Dacă a>0 funcția are un minim, vârful parabolei, V, de coordonate:

    V space open parentheses negative fraction numerator b over denominator 2 a end fraction comma fraction numerator negative increment over denominator 4 a end fraction close parentheses space comma space increment equals b squared space minus space 4 a c

    Dacă a<0 funcția are um maxim, vârful parabolei, V, de coordonate:

    V space open parentheses negative fraction numerator b over denominator 2 a end fraction comma fraction numerator negative increment over denominator 4 a end fraction close parentheses space comma space increment equals b squared space minus space 4 a c

    Problema: Se consideră funcția ƒ space colon space R space rightwards arrow space R comma space ƒ open parentheses x close parentheses space equals space m x squared space minus space 8 x space minus space 3 comma space space m element of space R to the power of asterisk times.  Să se determine valorile lui m știind că valoarea maximă a funcției ƒeste egală cu 5.

    Rezolvare: Dacă funcția are valoare maximă atunci m<0 şi valoarea maximă este

    y subscript m a x end subscript equals space minus space fraction numerator increment over denominator 4 a end fraction space rightwards double arrow space minus fraction numerator left parenthesis negative 8 right parenthesis squared space minus space 4 space asterisk times space m space asterisk times space left parenthesis negative 3 right parenthesis over denominator 4 m end fraction space equals space 5 space rightwards double arrow negative space fraction numerator 64 space plus space 12 m to the power of left parenthesis 4 end exponent over denominator 4 m end fraction space equals space 5 space rightwards double arrow rightwards double arrow negative space fraction numerator 16 space plus space 3 m over denominator m end fraction space equals space 5 space rightwards double arrow 16 space plus space 3 m space equals space minus 5 m space rightwards double arrow space 8 m space equals negative 16 space rightwards double arrow space m space equals space minus 2

    Intersecţia cu axele de coordonate:

    large intersection O x colon space minus d a c ă space increment greater or equal than 0 comma space x subscript 1 space equals space fraction numerator negative b minus square root of increment over denominator 2 a end fraction comma space x subscript 2 space equals space fraction numerator negative b plus square root of increment over denominator 2 a end fraction large intersection O y colon space x equals 0 comma space y equals b

    Problema: Să se calculeze distanța dintre punctele de intersecție ale graficului funcției ƒ space colon space R space rightwards arrow space R comma space ƒ open parentheses x close parentheses space equals space minus x squared space plus space 2 x space plus space 8 cu axa O x.

    Rezolvare: Punctele de intersecție ale graficului funcției cu axele de coordonate sunt x subscript 1 comma space x subscript 2 iar distanța dintre punctele de intersecție este open vertical bar x subscript 2 minus x subscript 1 close vertical bar

    Soluţiile ecuaţiei ƒ open parentheses x close parentheses space equals 0 space equals greater than negative space x squared plus space 2 x space plus space 8 space equals space 0

    increment space equals space 2 squared space minus space 4 space asterisk times space left parenthesis negative 1 right parenthesis space space asterisk times space 8 space equals space 4 space plus space 32 space space equals space 36 comma space x subscript 1 space equals space fraction numerator negative 2 minus 6 over denominator negative 2 end fraction space equals space 4 comma space x subscript 2 space equals space fraction numerator negative 2 minus 6 over denominator negative 2 end fraction space equals space 2. open vertical bar x subscript 2 space minus space x subscript 1 close vertical bar space equals space open vertical bar 2 minus left parenthesis negative 4 right parenthesis close vertical bar space equals space open vertical bar 6 close vertical bar space equals space 6.

  • ChemType pentru Moodle

    O derivată din MathType conceput pentru a vă ajuta să lucrați cu formule chimice.

    ChemType este o derivată a MathType concepută pentru a vă ajuta să lucrați cu notații și formule chimice. Editorul nostru vizual de formule chimice are o bară de instrumente cu simbolurile chimice comune și o experiență de utilizator adaptată domeniului chimie.

    Știm că editarea formulelor chimice este complexă, deci în fila din bara de instrumente principală veți găsi cele mai frecvente simboluri chimice utilizate, simboluri ale tabelului  periodic și instrumente adaptate notațiilor și formulelor chimice.

    MathType vine cu câteva caracteristici specifice pentru a crea cu ușurință formule chimice direct din browser. Toate caracteristicile legate de chimie sunt activate când bara de instrumente ChemType este activată.

    Când MathType este activat cu bara de instrumente pentru formule chimice, ne vom referi la aceasta cu denumirea directă ChemType. Domeniul de aplicare al ChemType este limitat la formule chimice care pot fi codate cu MathML.

    Aplicațiile MathType și Integrările MathType includ de obicei două pictograme pentru MathType, una pentru bara de instrumente matematică generică și alta pentru ChemType.

  • Paracetamol

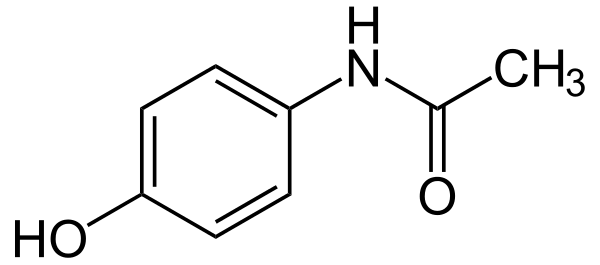
    Paracetamolul (sau paraacetilaminofenol, acetaminofen) este un derivat de para-aminofenol din clasa anilidelor, cu acțiune analgezică și antipiretică. Acțiunea sa antiinflamatoare este practic inexistentă, dar acest lucru nu înseamnă că nu poate fi folosit în durerile cauzate de inflamații.

    straight C subscript 8 straight H subscript 9 NO subscript 2